COMPRESSION & COMPACTAGE DES IMAGES
Une image est une matrice de ses couleurs ; en général, on considère des images 256 couleurs, c’est-à-dire que chaque pixel est codé en 8-bit.
Le but de la compression est de supprimer les redondances, c’est-à-dire de supprimer toute information non nécessaire. Ainsi, si il existe 256 couleurs différentes, il est peu probable qu’une image comporte toutes les couleurs possibles et on peut donc coder les pixels en moins de huit bits. On peut aussi exploiter les symétries de l’image pour mieux compresser et même approximer les images afin d’augmenter les redondances qu’elle comporte. On a alors une perte de qualité de l’image, on parle de compression destructive ou de compactage, que nous aborderons à peine.
I. Compression statistique
Au lier de coder chaque mot de code par un même nombre de chiffres, il est plus logique de coder les variables les plus fréquemment utilisées par le plus petit nombre de chiffres possible ; on peut alors utiliser une méthode très répandue, même aujourd’hui.
2.Méthode de Huffman [1951]
a. Méthode de Huffman
On classe les probabilités des mots de code par ordre décroissant, et on réunit entre elles les plus faibles probabilités jusqu'à ce qu'il n'en reste que deux. On donne alors à ces deux probabilités les noms 0 et 1, puis "on remonte". Cette méthode est très efficace et permet un réel gain, mais elle nécessite un dictionnaire afin d’être décodée, ce qui prend de la place et peut même conduire à un agrandissement du fichier. C’est pourquoi on a crée un classement moyen d’utilisation des caractères dans les différents pays (cas du texte), ce qui permet de se passer de dictionnaire, mais diminue évidemment la compression intrinsèque.
Exemple:
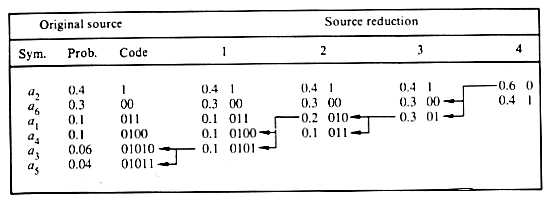
Lavg=0.4(1)+0.3(2)+0.1(3)+0.1(4)+0.06(5)+0.04(5)=2.2 bits/symbole,
H=0.4log2(0.4)+0.3log2(0.3)+0.1log2(0.1)+0.1log2(0.1)+0.06log2(0.06)+0.04log2(0.04)=2.14 bits/symbole,
donc 
=0.97.
Le codage de Huffman est donc très efficace, mais il nécessite un certain temps de calcul. En effet, une liste de A éléments différents nécessite A-2 réductions de variables et assignements de codes (254 pour une image en niveau de gris ou une composante d'une image RGB...).
C'est pourquoi on considère les méthodes suivantes, qui, bien que moins efficaces, sont plus rapides.
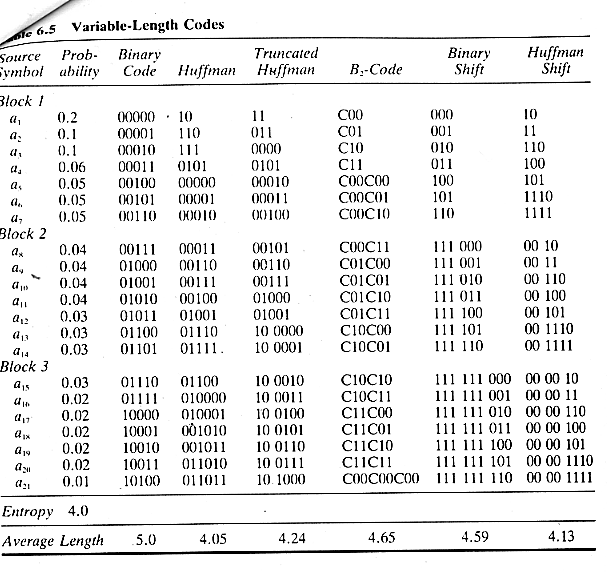
b. Méthode de Huffman tronquée
Afin de gagner du temps, on décide de négliger les pertes causées par un codage non optimum des variables les moins fréquemment utilisées. Au delà d'un nombre A donné d'éléments codés de manière optimale, on donne un code donné et on lui ajoute ensuite 1 pour obtenir les suivants. Les mots de code obtenus sont différents, puisque la liste de départ l'est.
c. B-code
On utilise C, le bit de continuation, pour séparer les mots de code les un des autres (C=0 ou 1, bien sûr); Le Bn-code est caractérisé par l'utilisation de n nombres entre deux bits de continuation. Dans l'exemple, on considère le B2-code. Ceci permet d’obtenir des mots de code non assimilables beaucoup plus rapidement que Huffman, mais ceux-ci sont plus longs à cause des bits de continuation.
d. Les codes de changements (Shift)
Ils nécessite le groupement de la source en blocs groupés par probabilités décroissantes. On considère dans l'exemple le code de changement 3-bit de la liste (d'où les 3 blocs). On utilise le fait qu’en 3-bit, les mots de code sont non assimilables jusqu’à 111, et que lorsque la probabilité décroît rapidement, on peut négliger les pertes dues à l’allongement des mots de code aux faibles probabilités.
Tableau récapitulatif des codes à longueur variable
II. Théorie de l’information
En pratique, plus un événement a de chances de se produire, moins il représente d’information, puisqu’on lui attribuera un mot de code d’autant plus court : On définit la quantité d’information I(E) de l’événement E par : I(E)=log(1/P(E))=-log(P(E))
[celle-ci est inversement proportionnelle à la probabilité de l’événement E.]
En effet, si un événement a 100% de chances de se produire, on ne lui attribuera pas d'information lors de la compression d'où I(E)=-log1=0.
La base du logarithme est déterminée par la base dans laquelle on travaille: en base 2, -log2(1/2)=1, c'est-à-dire qu'un bit peut représenter un événement ayant 50% de chances de se produire, ce qui est évident.
Imaginons qu'on génère une séquence aléatoire finie ou infinie dénombrable de symboles. Soit le symbole ai; on a I(ai)=-log[P(ai)]. Si on émet k symboles de la source, pour k assez grand, l’information totale sera (loi des grands nombres):
Donc l’information moyenne par symbole émis est 
.
On l'appelle incertitude ou entropie de la source (le nom entropie se justifie puisque une entropie quantifie le désordre ou l'incertitude d'un système). Elle s’exprime en bits/caractère.
Remarquons que cette théorie définit la quantité minimale moyenne de caractères assignable à un mot de code sans tenir compte du dictionnaire ; celui-ci va nécessairement pénaliser le codage et rendre la compression beaucoup moins efficace.
Ainsi, on a démontré qu’il existe une compression maximale atteignable : la longueur minimale du message sans dictionnaire est n.H où H est l’entropie de la liste et n le nombre de ses éléments. On définit donc naturellement l’efficacité d’un procédé de compression par :
, où L est la longueur est la longueur moyenne d’un mot de code dans un codage particulier. L’efficacité doit être aussi proche que possible de 1 inférieurement.
2.Premier théorème de Shannon
Il définit la longueur moyenne d'un mot de code accessible pour une transmission parfaite. Il démontre qu’en décomposant les caractères, et en les considérant en n-uplets plutôt qu’en éléments indépendants, l’efficacité du codage tend vers 1 quand n tend vers l’infini, et H(z’)=nH(z) où z’ est une liste déduite de z par n décompositions.
Exemple : P(a1)=1/3 , P(a2)=2/3 ; a1=0, a2=1 : 
=0.918
(-1/3log1/3-2/3log2/3=0.918)
Si b1=a1.a1, P(b1)=1/9 111
b2=a1.a2, P(b2)=2/9 10
b3=a2.a2, P(b3)=4/9 0
b4=a2.a1, P(b4)=2/9 110: 
=0.97
((3.2+1.4+2.2+3.1)/9=1.89)
On peut donc atteindre théoriquement un codage aussi bon que voulu... au prix du temps de calcul, et sans tenir compte du dictionnaire ; d’autre part, ces décompositions entraînent nécessairement une information supplémentaire afin de recomposer les éléments initiaux.
Le résultat à retenir est donc : il est *possible* d’atteindre un codage parfait, même si on ne sait pas le faire aujourd’hui à cause du problème du dictionnaire.
A priori, telle qu'elle a été présentée, l'entropie ne sert qu'à estimer l'efficacité de la compression, mais en pratique elle a une fonction fondamentale dans la compression graphique: elle n'a en effet pour l'instant pas été définie pour une image, mais pour une couleur, par exemple. En réalité l'entropie d'une image est l'entropie minimale qui peut être obtenue en considérant ses pixels de différentes manières.
En effet, si une image a de fortes symétries, considérer des paires de couleurs au lieu de couleurs donnera une entropie plus faible, et donc une meilleure compression. Le fait que la différence entre ces deux entropies soit non négligeable est même une condition suffisante de symétrie...
En fait, on prouve qu'en augmentant la taille du bloc de pixels considéré, l'entropie tend vers l'entropie de l'image, mais a cause du temps de calcul, on se contente de calculer les entropies du premier et du second ordre...
Rques:
Exemple: Estimons l'entropie de l'image 8-bit donnée par la matrice:
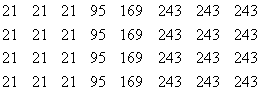
On obtient le tableau suivant:
|
Couleur |
Nombre |
Probabilité |
|
21 |
12 |
3/8 |
|
95 |
4 |
1/8 |
|
169 |
4 |
1/8 |
|
243 |
12 |
3/8 |
On a: H=-(3/8ln3/8+1/8ln1/8+1/8ln1/8+3/8ln3/8)/ln2=1.81 bits/pixels.
(On a log2(x)=ln(x)/ln2)
Considérons le tableau des paires:
|
Paire de couleurs |
Nombre |
Probabilité |
|
(21,21) |
8 |
¼ |
|
(21,95) |
4 |
1/8 |
|
(95,169) |
4 |
1/8 |
|
(169,243) |
4 |
1/8 |
|
(243,243) |
8 |
1/4 |
|
(243,1) |
4 |
1/8 |
H=2.5/2=1.25 bits/pixel.
Le gain d'entropie crée par les symétries si on considère deux pixels au lieu d'un est donc de 1.81-1.25=0.56 bits/pixels. Le gain par symétrie n'est donc pas négligeable et on ne peut se contenter de la compression à mots de code à longueur variable.
III. Compression spécifique aux images
On peut utiliser les symétries d’une image afin d’améliorer encore la compression.
Tout nombre binaire peut être décomposé en un polynôme de IR[2] (de même que tout nombre décimal peut être décomposé en un polynôme de IR[10] dont les coefficients sont ses chiffres); si a est une couleur d'une image m-bit:
a=am-12m-1+am-22m-2+...+a121+a020
ainsi, 7310=10010012=1
26+025+024+123+022+021+120
On peut donc décomposer une image m-bit en m "sous-images" 1-bit. Les redondances sont alors beaucoup plus importantes, puisque l'image ne comporte que des 0 et des 1 contre au maximum 256 symboles différents dans l'image de départ.
Cependant, cette décomposition canonique n'est pas la seule a être utilisée, puisque elle est imparfaite; par exemple, 127 (01111112) et 128 (10000002), deux couleurs proches, ne sont équivalentes dans aucun plan décomposé. On définit donc la décomposition grise (Gray code). Le code Gray m-bit 
correspondant à 
est défini par:
gi=ai
ai+1 0
m-2 où représente le ou exclusif.
gm-1=am-1
Pour 0111111, le Gray code est: 01000000
Pour 1000000, le Gray code est: 11000000
Ainsi, le code Gray a la propriété que deux mots de code successifs ne diffèrent que d'un bit.
Dans les paragraphes suivants, on considère l'image décomposée en ses plans de bits, ce qui permet de ne considérer que deux valeurs des pixels: 0 ou 1.
Cette méthode s'applique de manière efficace lorsque de nombreux pixels contigus ont la même valeur. L'idée de base est de subdiviser l'image en blocs qui peuvent être de couleur blanche, noire ou mélangée. La catégorie la plus probable est alors codée par 0, la suivante par 10, et la dernière par 11. Bien entendu, le symbole représentant la couleur mélangée n'est utilisée que comme un préfixe, suivi par l'expression explicite du contenu du bloc.
On peut optimiser cette méthode dans des cas particulier; le plus fréquent est celui exploité par le WBS (White Block Skipping): dans le cas de textes, par exemple, la couleur majoritairement représentée est le blanc, le noir et la couleur mitigée étant alors négligeables. On décide alors de coder les surfaces blanches par 0 et les autres par 1 suivi par l'expression explicite du contenu du bloc.
L'application de cette méthode nécessite bien sûr le choix des blocs; deux méthodes sont alors utilisées; soit on décompose l'image en blocs 1n (lignes) (ou n1...), soit (cas du WBS) on décompose l'image en blocs de plus en plus petits; la réduction des blocs se poursuit jusqu'à ce soit le bloc soit blanc (codé par 0), soit qu'une taille minimum prédéfinie de bloc soit atteinte, et le bloc est alors codé par 1 suivi de l'expression explicite de son contenu.
Cette technique a été développée dans les années 1950 et est aujourd'hui, avec ses extensions deux dimensions que nous verrons dans le d., couramment utilisée dans les FAX.
Elle consiste à décomposer l'image en ses lignes, et à annoncer le nombre de pixels noirs, le nombre de pixels blancs, etc... L'image est alors parfaitement déterminée. Pour raccourcir cet énoncé, on commence toujours par annoncer un nombre de pixels blancs (quitte à ce que ce soit 0). On peut ensuite coder les run-length eux-mêmes par un codage à longueur de code variable. On peut alors estimer l'entropie run-length de l'image:
Si aj représente une alignement noir de longueur j, on peut estimer la probabilité que aj soit émis par une source imaginaire alignements noirs de longueur j en divisant le nombre d'alignements noir d de longueur j dans l'image entière par le nombre total d'alignements noirs. L'entropie de la source imaginaire est alors H0, donnée par la définition de l'entropie. De même, soit H1 l'entropie de la source imaginaire alignements blancs; l'entropie run-length de l'image est alors: 
, si L0 et L1 sont les longueurs moyennes des alignements noirs et blancs.
[SCHEMA]
On peut s’intéresser aux formes composant un dessin ; dans le cas d’un disque, il suffit de rallonger chaque ligne d’un pixel de chaque côté, puis d’en enlever.
Le tracé direct de contour garde la coordonnée des pixels supérieurs du bloc, et à chaque ligne, D ’ et D ’’ où D ’ est l’écart entre le début d’une ligne adjacente et de la ligne considérée et D ’’ la longueur de la portion noire.
Le codage double delta conserve lui aussi les pixels supérieurs, mais D ’ et D ’’’ où D ’’’ est l’écart entre la fin de ligne et une fin de ligne adjacente.
c. Prédiction corrigée
On peut aussi extrapoler la valeur d’un pixel à partir de ceux qui lui sont adjacents et corriger l’erreur. Il suffit ainsi de stocker la fonction qui a permis l’extrapolation et l’erreur commise. Cette dernière constitue une nouvelle image qui peut alors être compressée par l’une ou l’autre des méthodes étudiée, mais la méthode d’Huffman reste la plus souvent utilisée. L’avantage est que si l’image est bien extrapolée, l’erreur est souvent très proche de zéro, ce qui permet une compression importante de celle-ci. Les fonctions d’extrapolation généralement utilisées sont des polynômes en les pixels précédents de la même ligne ou même, en 2-D, des pixels autour du pixel considéré ; ces méthodes nécessitent généralement la conservation des k premiers pixels de l’image comme conditions initiales.
C’est une bonne méthode de compression, même si, pur une image m-bit, l’erreur conservée doit être stockée en m+1 bit (elle peut être négative).
On peut aussi utiliser des symétries ou des relations apparentes entre un pixel et ses voisins.
On définit un facteur de corrélation dont la formule explicite a peu d’intérêt : seul nous intéresse ici le principe.
g (D
n)=A(D n)/A(0) avec A(D n)=
On fait varier y à x fixé et lorsque f(x,y+D n)» f(x,y), g (D n) est proche de 1.
Cette méthode permet de rationaliser la recherche de ces symétries; elle peut parfois suggérer le type de prédiction à utiliser.
2.Compression destructive
C’est la prédiction corrigée si on ne conserve pas l’erreur commise.
On peut négliger les coefficients du DSF faibles, ce qui permet la synthèse d’une image simplifiée.
On peut annuler les coefficients du DSF voulus, ce qui permet de simplifier l’image, mais peut occasionner une énorme perte de qualité.
3.Risques d'erreur de transmission
a. 2eme Théorème de Shannon (1948)
Il s'applique aux transmissions sur lignes perturbées. Il précise qu’il existe des codages permettant d’atteindre un taux d’erreur inférieur a tout e donné.
Par exemple, si au lieu de transmettre 0 ou 1, on transmet 000 et 111, et si, si il y a une erreur on choisit le symbole majoritairement représenté, la probabilité d'erreur est la somme des probabilités de 2 erreurs et de 3 erreurs, soit, si la probabilité d'erreur est pe: pe3+3pe2(1-pe), et si on augmente le nombre de répétitions, elle est aussi petit que l'on veut.
b. Méthode de Hamming
Afin d'éviter les erreurs que pourrait créer un mauvaise transmission des données, on choisit souvent des codes dont la distance est supérieure ou égale à 3 (d(101101,011101)=2). C’est cependant difficle compte tenu du fait que ces codes doivent rester non assimilables ; on préfère utiliser la méthode de Hamming : on crée un code, puis on lui applique cette méthode, qui en crée un nouveau, plus long, plus sûr.
Méthode de Hamming: Exemple d'un code de Hamming 7-bit associé à un code 4-bit:
est associé à 
avec:
h1=b3b2b0
h2=b3b1b0
h3=b3
h4=b2b1b0
h5=b2
h6=b1
h7=b0
Où représente le ou exclusif; des comparaisons simples permettent de s'assurer qu'il n'y a pas eu d'erreur de transmission.
Rque: 00=1;01=10=1;11=0
La redondance du code augmente et le taux de compression diminue d'autant, mais la sûreté de la transmission est assurée, ce qui n'était pas le cas avant la compression.
Sources: